This page is for archival purposes only!
Students should use
ODTU-Class
There will be 28 lectures given by the instructors, each lasting 2 hours. The schedule below gives a rough list of course content on a per-week basis.
Note: This schedule may be modified/reorganized as the class progresses.
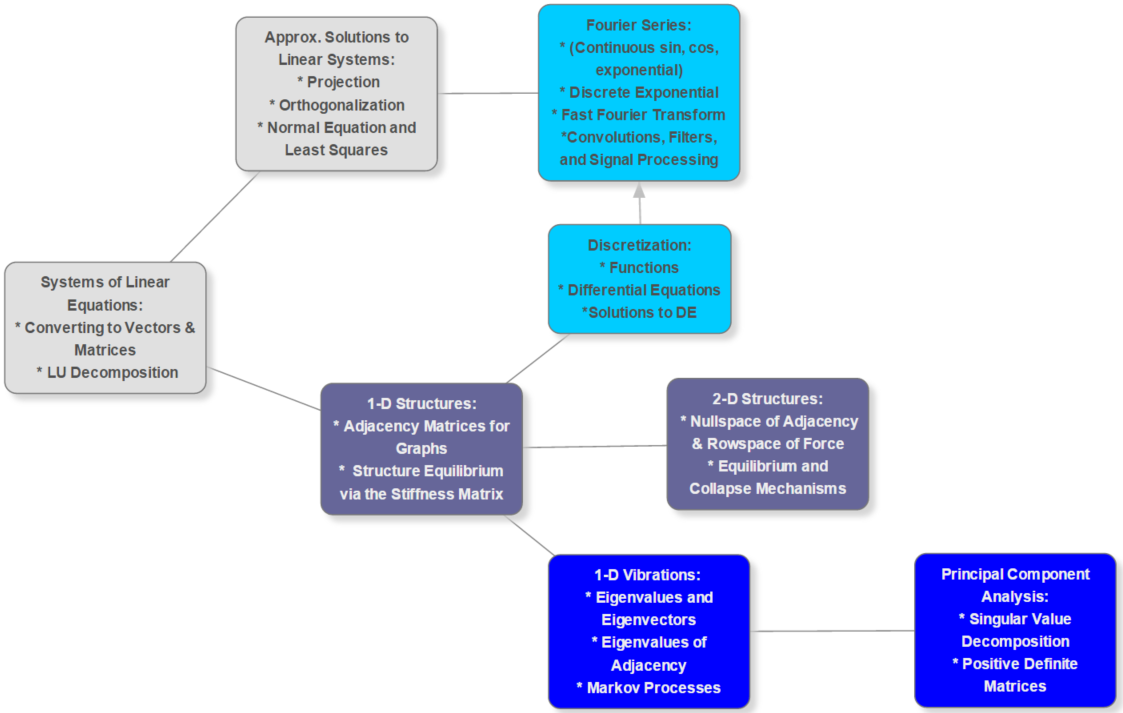
| Week 1 |
Systems of Linear Equations. Converting to Vector and Matrix Equations Computing the LU-Decomposition of a Matrix Solving Matrix Equations Using LU-Decomposition |
| Week 2 |
Approximate Solutions of Linear Systems. Projection and Orthogonalization (QR-Decomposition) Normal Equation and Least Squares Approximation |
| Week 3 |
1-Dimensional Structures. Adjacency Matrices (Edge-Edge, Edge-Node, Node-Node) Structure Equilibrium via the Stiffness Matrix. |
| Week 4 |
2-Dimensional Structures. Nullspace of Adjacency Matrix and Rowspace of Force Matrix Structure Equilibrium and Collapse Mechanisms |
| Week 5 |
1-Dimensional Vibration. Eigenvalues and Eigenvectors (Diagonalization) Eigenvalues of Adjacency Matrix Markov Processes |
| Week 6 |
Principal Component Analysis. Singular Value Decomposition Positive Definite Matrices |
| Weeks 7-9 |
Discretization of Functions. Initial Value Problems and Euler's Method Matrices Corresponding to Differentiation Operators Boundary Value Problems and Discretization of Differential Equations Inverses and Delta Functions |
| Week 10-14 |
Fourier Series (Projection onto sin, cos, Complex Exponential) Continuous and Discrete Fourier transforms Fast Fourier Transform Convolution, Filters, and Signal Processing |
